OK. I am about to do something. Let’s see if I can pull it off.
Mathematics was something I always hated. I always saw my friends excel at it, and that disappointed me sitting with fewer marks than them. Well, right now, I am going to attempt to summarize the al the concepts of mathematics from the 1st standard to the 12th standard using the concept of the number line.
Broadly, the mathematics syllabus can be summarized in the following chapters: Basic Arithmetic, Fraction, Decimals, Basic Geometry, Area and Perimeter, Integers, Exponents and Power, Mensuration, Coordinate Geometry, Trigonometry, Calculus, Complex Number, Functions, Matrices, and Vectors.
So, you are a six-year-old kid, it’s the first day of school and you get introduced to this “wonderful” subject that you will curse your whole life: Mathematics or simply, Maths. Sometime in the 1st standard, you are introduced to the concept of the number line. In the above-listed chapters, starting from Basic Arithmetic to Decimals, we are simply walking on the positive side of the number line. Let’s take the example of addition. The addition is simply, “adding” or moving right of the number line. We know that 1+3-4. But why? Why not 4, or 7, or 1? The expression 1+3 means, if you are at position 1 of the number line, where will you be, if you moved 3 steps to the right? We will be at position 4, hence we write 1+3=4. Similarly, subtraction is the opposite of addition, i.e. moving left of the number line. However, up to Decimals, the left side of the number line is kept hidden from us. We are made to walk only on the right of the number line. The multiplication and division operations are simple efficient methods of representation on additive and subtractive operations. For example, 2*5=10. But why? Well, it is the result of adding 5, 2’s together, i.e. 2+2+2+2+2=2*5=10. I mean, imagine having to write 2, 100000’s using the addition notation. It will be as big as a book. Writing 2*1000 is efficient. So is true for division.
By the 5th standard, we are introduced to the other half of the number line: the negative side. Thus, introducing the concept of integers. We are taught some “rules”.
-1x-1=1
-1x1=-1, or 1x-1=-1
1x1=1
All the above expressions can be proved using the number line. Similarly, fractions are the numbers lying between the whole numbers. Concepts such as exponents are more efficient methods of representation. Just as multiplication notation made it easier to represent long addition, exponential notations made it easier to represent repetitive multiplications.
So far, we have completed the math syllabus till the 5th standard. Somewhere in between, we are introduced to another number line, which is perpendicular to the previous horizontal number line. Thus, introducing topics such as geometry, area and perimeter, and coordinate geometry. If we connect to coordinates we get a line, which can be represented using vectors and matrices. If we connect two coordinates diagonally, we can use trigonometric functions to determine the length of other line segments. Still, we are playing with the number line.
10 years of mathematics is summarized here for you. Everything till here is on the number line and the interplay of coordinates.
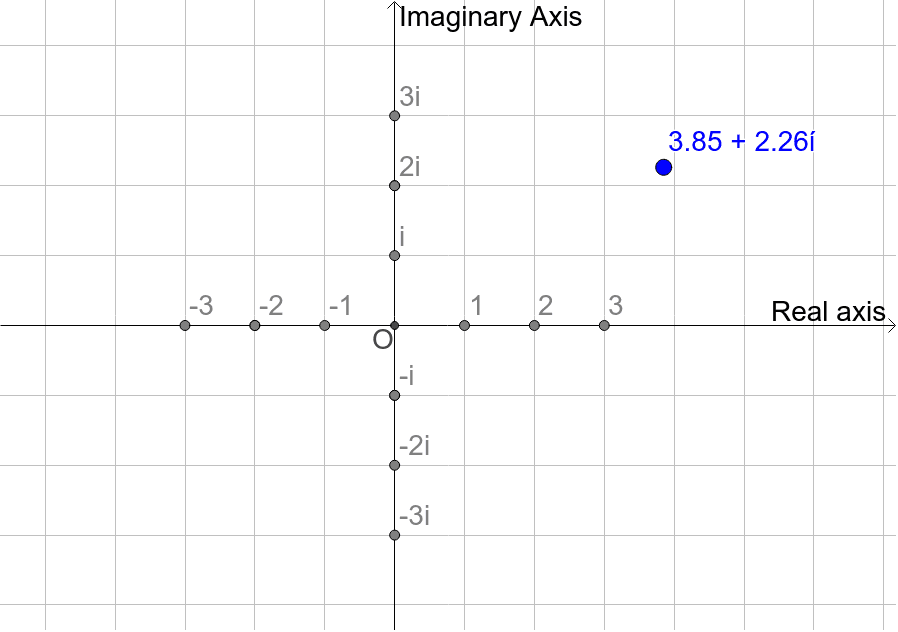
Enter calculus. All the operations of calculus involve playing with the coordinates. However, complex numbers looks ferocious from the distance but cute and cuddly up close. Unlike the previous vertical number line which was a replica of the horizontal number line, the complex number line is a vertical line with coordinates of ‘n’ time square root of negative one, or n*sqrt(-1) a.k.a ‘i’, bidirectionally.
This was a futile attempt to condense the world of mathematics in terms of the number line.
For further understanding:
https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
https://www.youtube.com/playlist?list=PLZHQObOWTQDMsr9K-rj53DwVRMYO3t5Yr
P.S. Things have been tumultuous lately. Hence, the delay. Apologies for that.